SQUAB
A Fast Benchmarking Software
for Surface Quantum Computing Architectures

Here, three standard layouts for planar surface codes are constructed step by step. Then, we provide two constructions of hyperbolic tilings. We consider Bravyi-Kitaev tiling, a square-octogonal tiling, and a rotated square tiling punctured with holes, that we call diamond holes architecture.

• Bravyi-Kitaev tiling
• Square-octogonal tiling
• Diamond holes tiling
• Hyperbolic tilings

Bravyi-Kitaev tiling

---

• Start by constructing a 5x5 square tiling and draw it to see the indices.
  >>Tiling 4 5 5
>>Draw
  
  



• Then, open the left side by opening a thin rectangle from v0 to v30 and open a rectangle between v10 and v35 on the right side.
  >>HoleRectOpen 0 30
>>HoleRectOpen 10 35
>>Draw
  
  
  
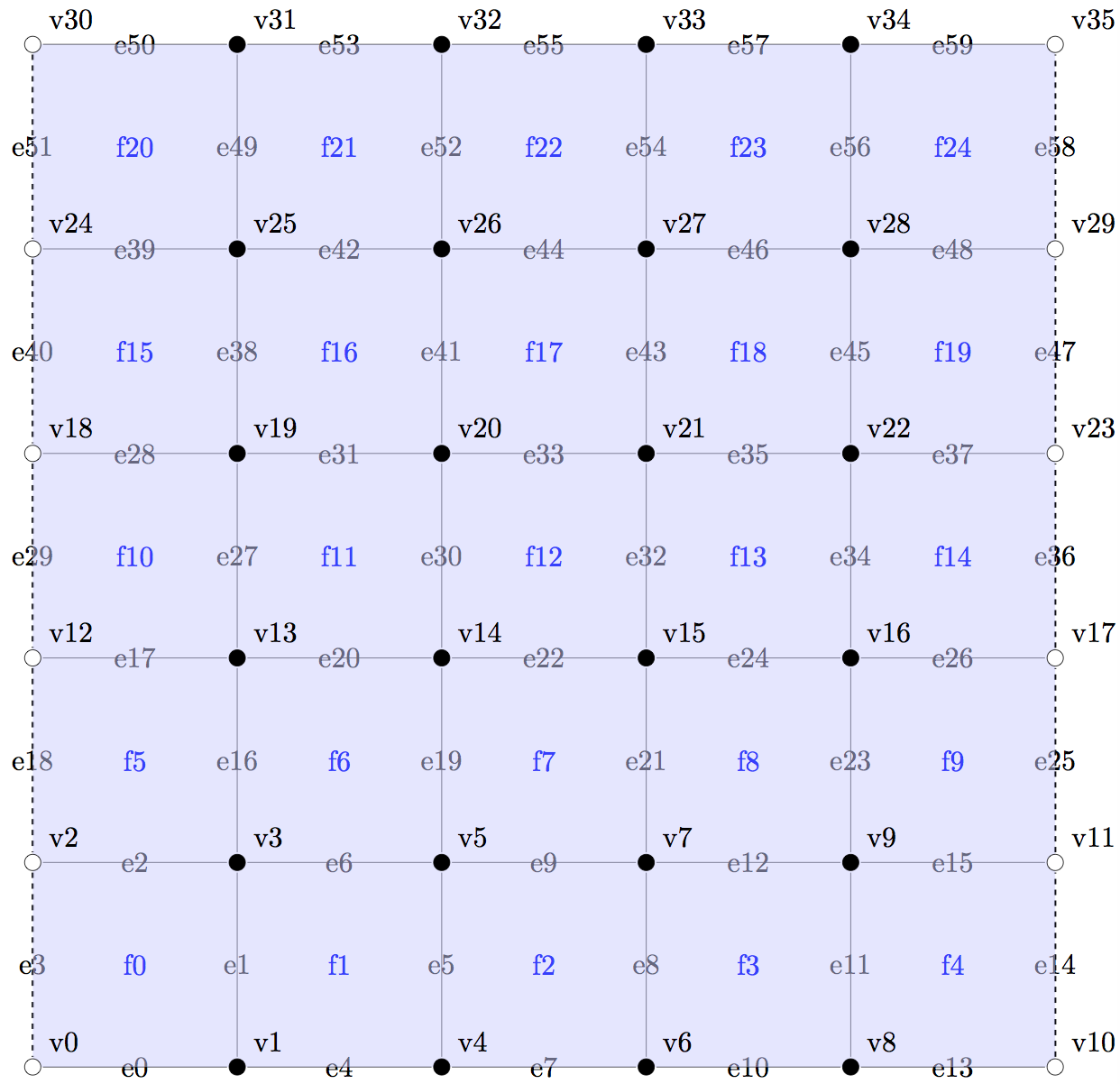
  This is Bravyi-Kitaev's lattice!

Square-octogonal tiling

---

• First create a grid of vertices and draw it.
  >>Grid 5 5
>>Draw
  
  



• Then add a octogon face using vertex indices
  >>AddFace 8 16 22 27 26 19 13 8 9
>>Draw
  
  



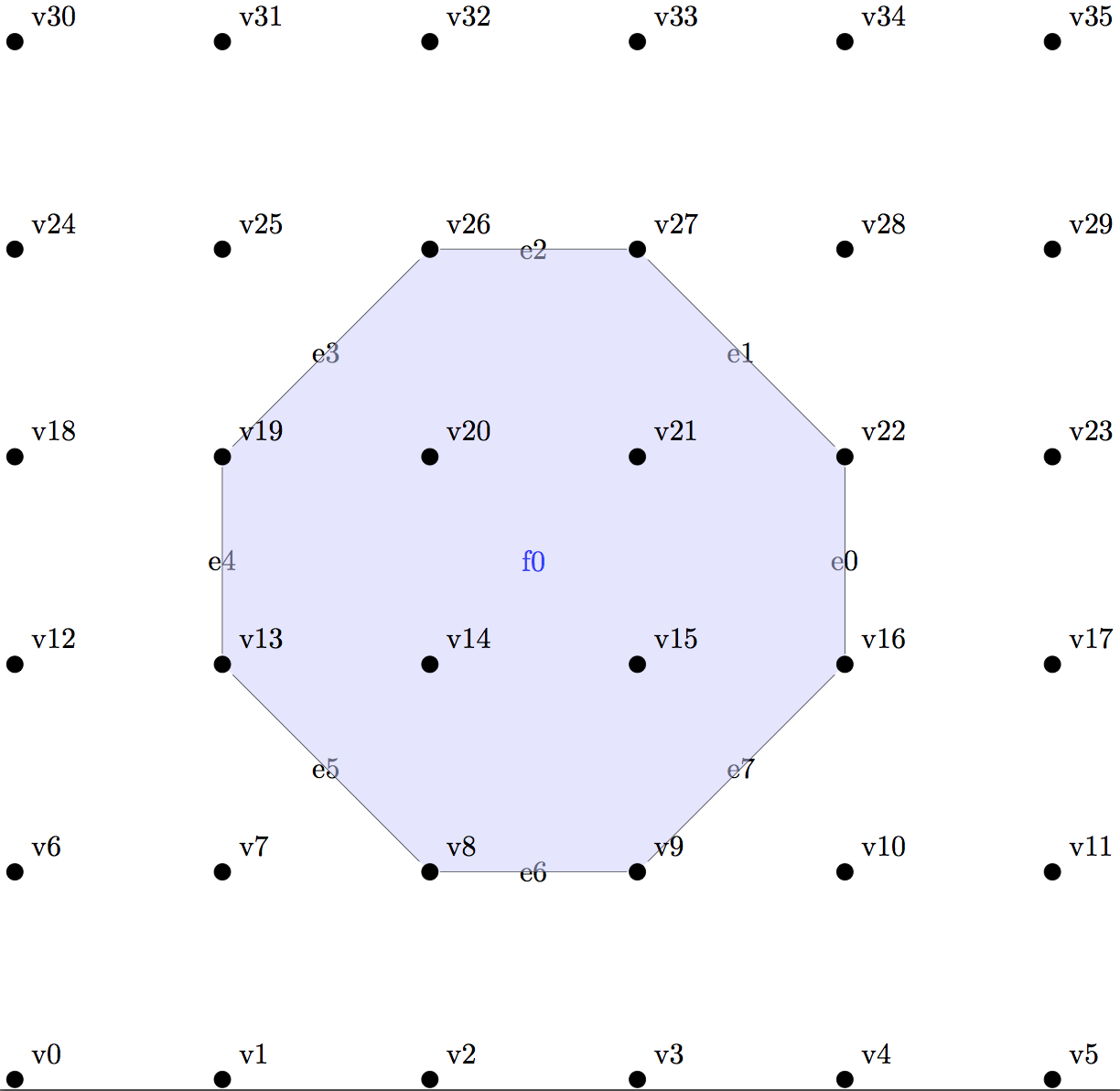
• and add 4 square faces around this octogon.
  >>AddFace 4 16 17 23 22
>>AddFace 4 26 27 33 32
>>AddFace 4 12 13 19 18
>>AddFace 4 2 3 9 8
>>Draw
  
  



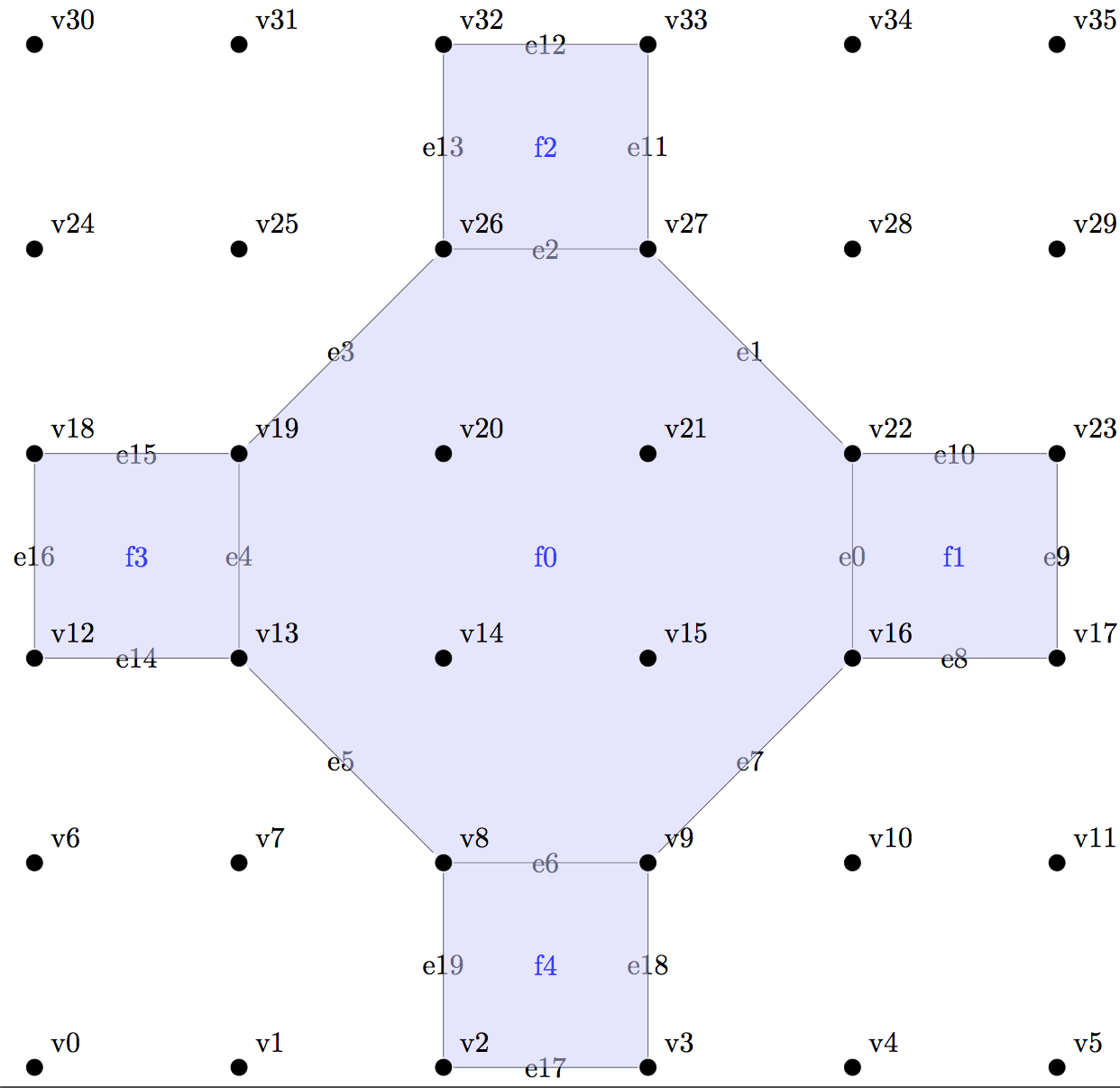
• We can now use the previous graph as an elementary tile and construct a periodic from it. For instance, if translate 3 times with vector (2,2) and 3 time along (-2,2), we get
  >>Translate 3 2 2
>>Translate 3 -2 2
>>DrawMin
  
  



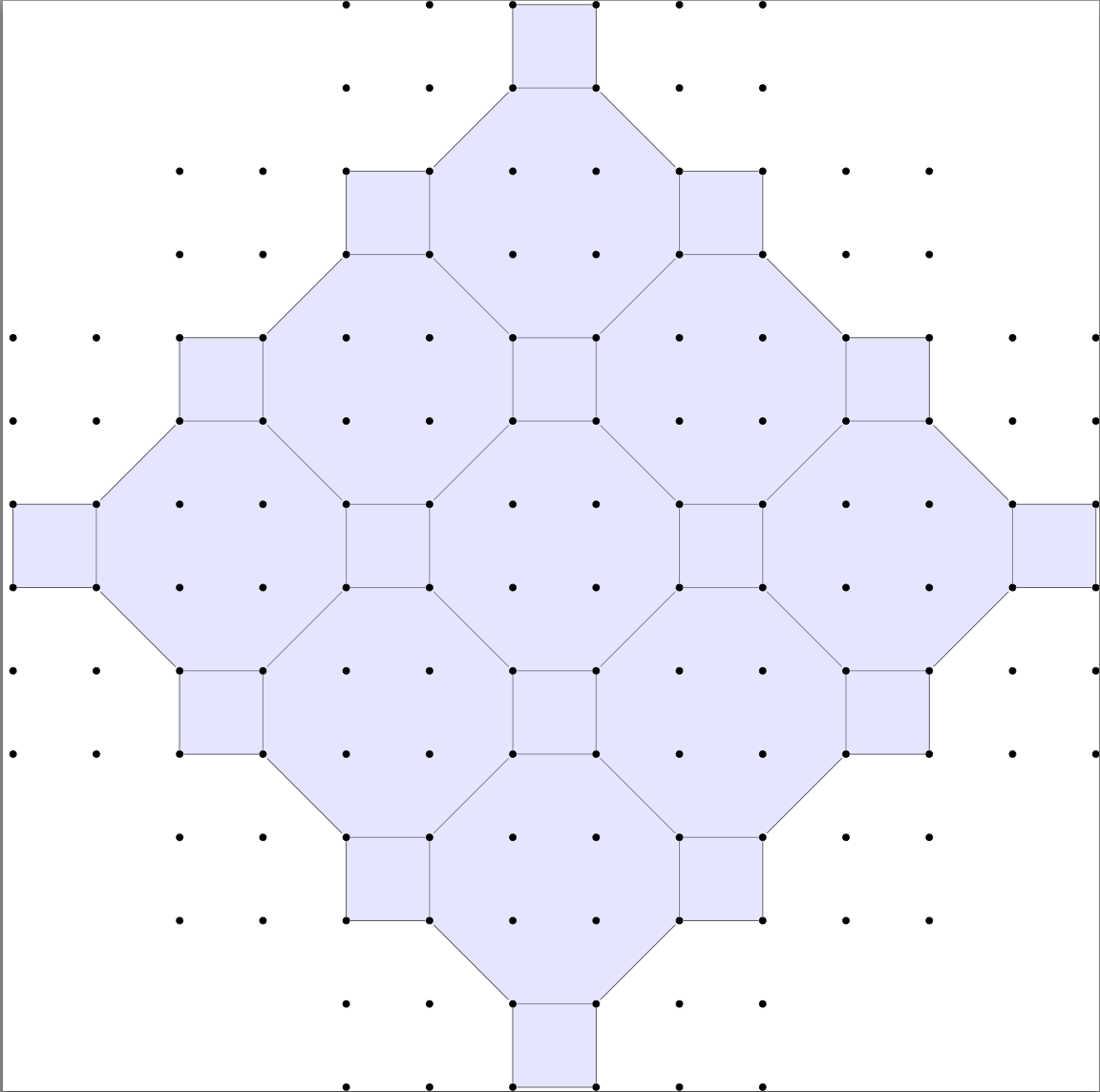
• Overall, we constructed a square octogonal tiling by
  >>Grid 5 5
>>AddFace 8 16 22 27 26 19 13 8 9
>>AddFace 4 16 17 23 22
>>AddFace 4 26 27 33 32
>>AddFace 4 12 13 19 18
>>AddFace 4 2 3 9 8
>>Translate 3 2 2
>>Translate 3 -2 2
>>CleanV
>>DrawMin
  
  
  
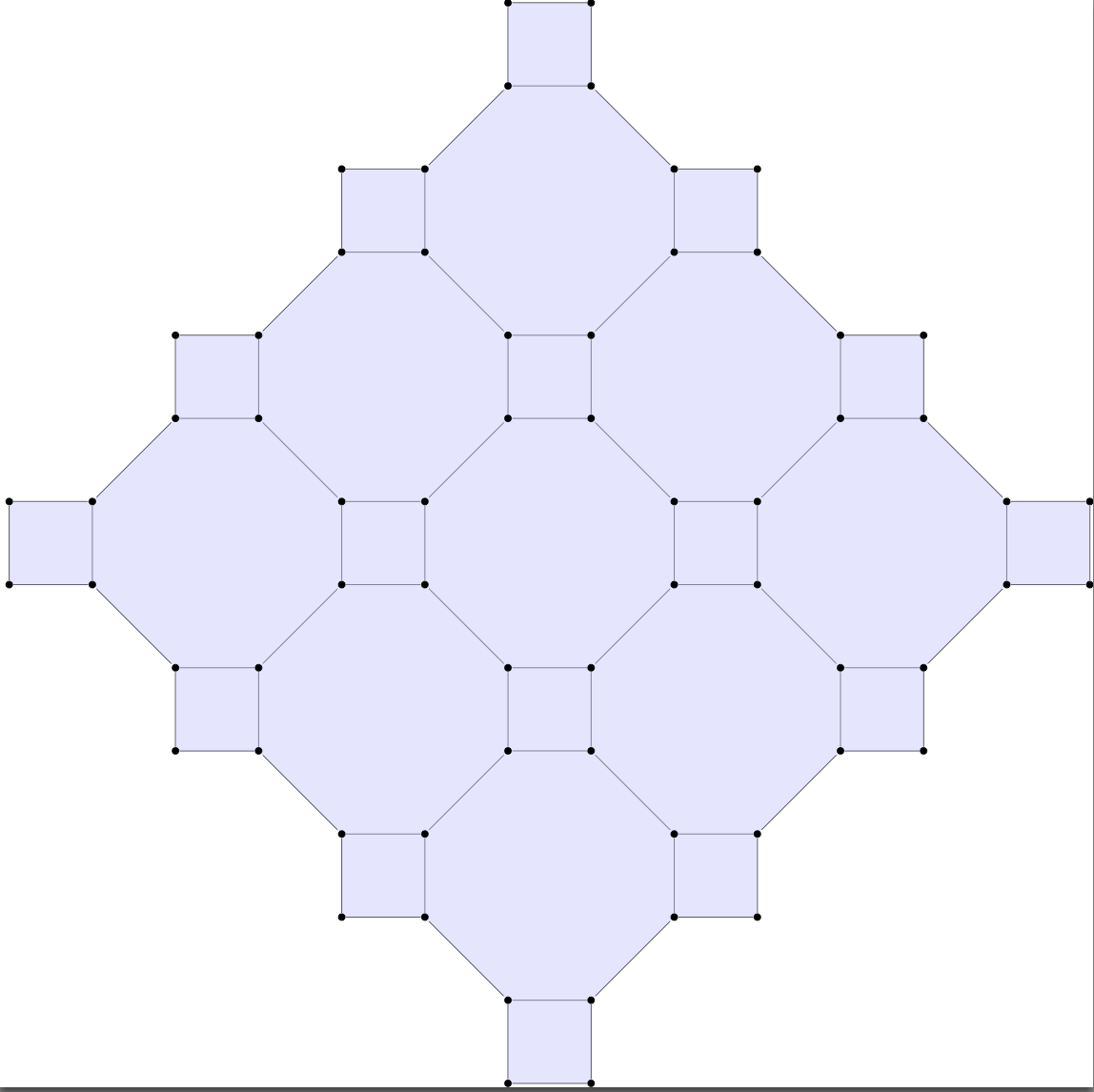
  The command CleanV is only used to remove useless vertices.



• To show the dual tiling use
  >>DrawDualMin
  
  
  
  

Diamond holes tiling

---

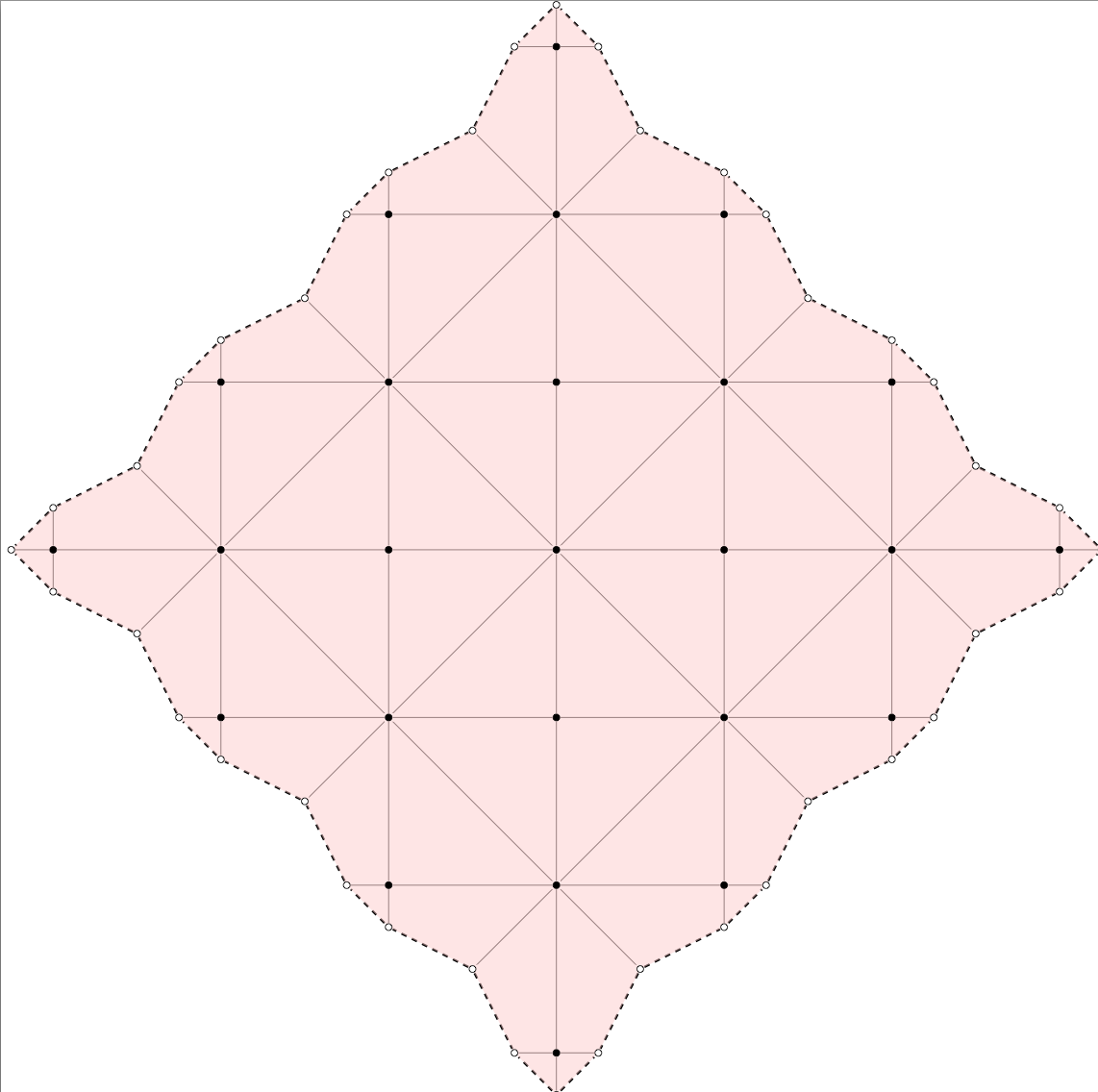
• First, create a small patch of a rotated square tiling. We start with a square that we replicate 4 times:
  >>Tiling 4 1 1
>>Translate 2 1 1
>>Translate 2 -1 1
>>Draw
  
  
  
  Then, add the missing face in the center.
  >>AddFace 4 2 3 5 9
>>Draw
  
  



• To obtain a 13x13 tiling, it suffices to translate the small patch.
  >>Translate 12 1 1
>>Translate 12 -1 1
>>Draw
  
  



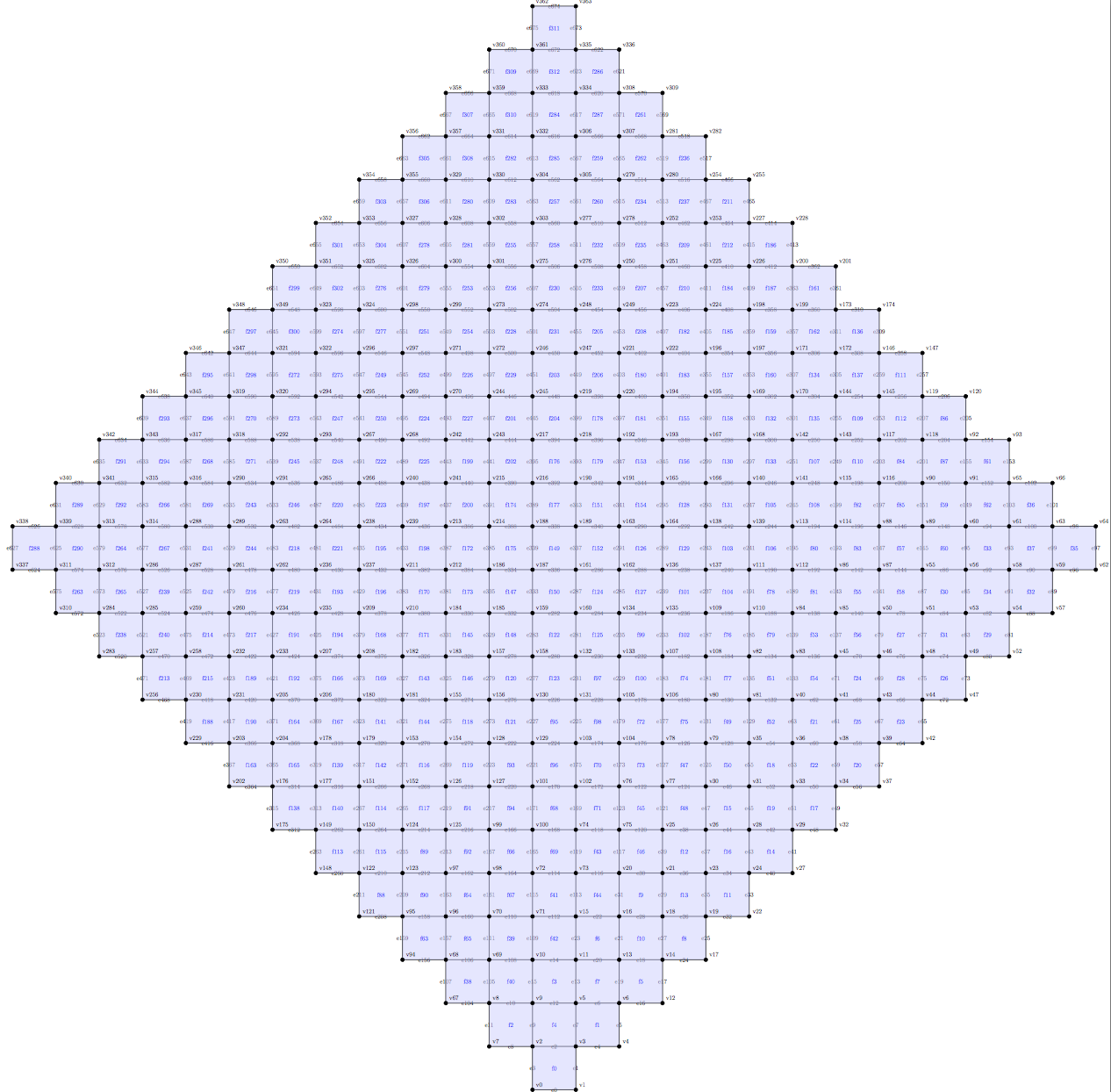
• Zoom in to find the faces to remove.
  >>HoleList 5 149 150 152 175 177
>>DrawMin
  
  
  
  This is our 1-qubit patch! Now translating by (7,7) and (-7,7) produces a tiling of the diamond hole architecture.



• For instance, here is a 6-qubits tiling.
  >>Translate 3 7 7
>>Translate 2 -7 7
>>DrawMin
  
  
  
  Once the patch is constructed, we can obtain a family of codes by constructing a periodic version of it using Translate. We do not need to draw it anymore. We can check the parameters of the code to verify the number of logical qubits is correct.



• With the previous example, we find 6 logical qubits, one per hole, as expected:
  >>Code
  
  
  
  If instead, we repeat the 1-qubit patch 10 times in both directions, we obtain a tiling of 22 000 qubits encoding 100 logical qubits:
  >>Translate 10 7 7
>>Translate 10 -7 7
>>Code
  
  



• Overall, the diamond hole patch is obtaine by:
  >>Tiling 4 1 1
>>Translate 2 1 1
>>Translate 2 -1 1
>>AddFace 4 2 3 5 9
>>Translate 12 1 1
>>Translate 12 -1 1
>>HoleList 5 149 150 152 175 177
  
  Then, you can saved this patch to use it later using the command Save with for instance >>Save diamond_patch
  saves this tiling in the folder saved_tilings under the name diamond_patch. One can quit the program and load it later using Load.
  
  Given this patch, translations of vectors (7,7) and (-7,7) generate a periodic tiling.





Hyperbolic tilings

---



• Hyperbolic tilings, which are not planar, cannot be constructed within our interface. Nevertheless, one can construct the files defining edges and faces of the graph using a more appropriate software and load these tilings using the command Load.
  This procedure is detailled in the webpage Upload your own tilings.
  
  The performance of two families of hyperbolic codes based on trivalent tilings and based self-dual tilings are plotted in our paper. These tilings as well as the Magma code used to construct them can be downloaded below.



• The trivalent hyperbolic tilings considered here have degree 3 and faces of length l and 2m and they depend on a prime number p. We denote these tilings by l_m_p_trivalent_hyp. The following Magma program generates the 2 text files:
  
  l_m_p_trivalent_hyp_edges.txt
  l_m_p_trivalent_hyp_faces.txt
  
  encoding respectively edges and faces of the tiling. As an example the first tilings of the family 6_6_p_trivalent_hyp are provided here.
  
  
  • Magma code for hyperbolic trivalent tilings
  • The family 6_6_p_trivalent_hyp
  
  These trivalent hyperbolic tilings were used by Zémor in 2009 in this article.



• The self-dual hyperbolic tilings consider here have degree m and faces of length m and they depend on a prime number p. We denote these tilings by m_p_selfdual_hyp. The following Magma program generates the 2 text files:
  
  m_p_selfdual_hyp_edges.txt
  m_p_selfdual_hyp_faces.txt
  
  encoding respectively edges and faces of the tiling. As an example the first tilings of the family 6_p_selfdual_hyp are provided here.
  
  
  • Magma code for hyperbolic selfdual tilings
  • The family 6_p_selfual_hyp
  
  
  These selfdual hyperbolic tilings were used by Delfosse and Zémor in 2012 in this article.